Do Real Gases Behave Ideally?

In the last post we have discussed the reasons behind the non-ideal behaviour of real gases. As we behave ideally in certain conditions, real gases also do. What are those conditions in which real gases behave like an Ideal gas?

As you know intermolecular forces are responsible for the non-ideal behaviour of real gases. So think about those situations in which these forces have no significance. Inter molecular forces are effective within a small range, if we increase the distance between two molecules, Inter molecular forces will diminish.    

In Boyle’s Law you have learnt that at lower pressure the volume of gas increases, which in turn increases the distance between molecules and in the larger space, volume of molecules can be neglected.  So by decreasing pressure we can beat attractive force by increasing the distance.

But still molecules are not completely free from attractive force; there are chances that they can be affected by the attractive force if any of them passes a nearby molecule. To cancel this possibility of getting caught by attractive force of nearby molecule, we have to increase the speed (or kinetic energy) of molecules and to increase their kinetic energy we have to increase temperature. At higher temperature molecules travel with higher speed and wouldn't get caught by other molecule.

That means at lower pressure and higher temperature real gases behave like an ideal gas. The temperature at which a real gas obeys Boyle’s law is called the Boyle’s temperature or Boyle’s point. Boyle’s point of gas depends on it’s nature.

Now we know how we can modify conditions to force real gases to behave ideally. Can we measure their deviation from ideal behaviour?

We know in Ideal gas equation:

 pV = nRT

pV/ nRT = 1

For an ideal gas the ratio of pV/ nRT is equal to 1. But in case of real gases this ratio deviates from unity. This ratio is defined as ‘Compressibility Factor’ and denoted as Z.

pV/ nRT = Z

When a graph is plotted between Z and pressure, we get a straight line for ideal gas. And for real gases we get different curves showing positive or negative deviation from straight line.

If we derive another equation from it, you will be able to understand the Compressibility Factor better.

pV/ nRT = Z

if we write V as V_real

p V_real / nRT = Z

From ideal gas equation we know:

pV_ideal = nRT

V_ideal = nRT/p

Now place the value of nRT/p in the above equation:

V_real / V_ideal = Z

In a graph of Z vs Pressure for ideal gas, we get a straight line at Z=1 which is parallel to the x axis. It doesn’t mean that with increase in pressure no changes occur to ideal gas, changes occur but these changes occur in such a manner that the ratio of pV/nRT remains unity.

While in case of real gases these changes occur in undisciplined way and the ratio of pV/nRT deviates from unity. Most of the real gases show a three staged curve where they have Z ≈1 at lower pressure, Z < 1 at high pressure and Z > 1 at a still higher pressure.

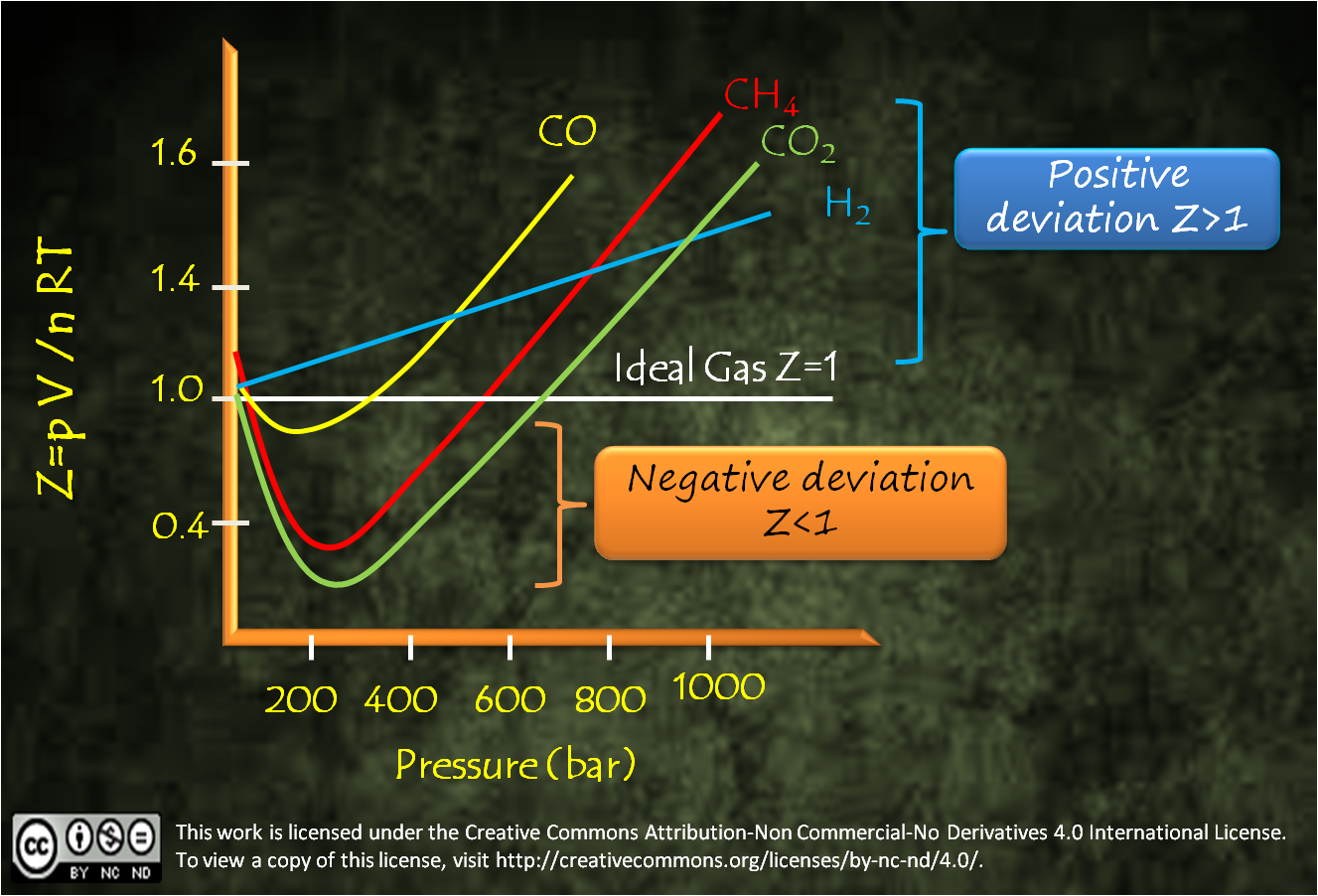
Stage I:  At lower pressure where Z ≈ 1 all gases show ideal behaviour. As pressure increases most of the real gases show negative deviation where Z < 1, which means V_real is less than V_ideal which signifies that the gas gets compressed more than the ideal gas at increased pressure. Here first time real gases start disobeying the Boyle’s law (p ∝ V^-1).

Stage II: As the pressure further increases, all real gases touch the straight line for an instance when they have Z= 1 and where they behave ideally since V_real is equal to V_ideal. 

Stage III: As the pressure reaches to still higher range, all real gases again deviate from ideal behaviour and show positive deviation where Z > 1. At this stage V_real is more than V_ideal that means the gases no more follow the trend of Boyle’s law of decrease in volume on increasing pressure. At this stage real gases again start disobeying the Boyle’s law (p ∝ V^-1) and it becomes impossible to compress them. 

Now you understand that why real gases obey Ideal gas equation at lower pressure and higher temperature. Does this information benefit to us? In the next post we will see how we can use it in practical life?​

Related Posts-

• Mole: A unit of measurement
• What is Avogadro's Hypothesis? 
• Gas Laws: Boyle’s Law
• Boyle’s Law and Its Applications
• GasLaws: Charles’ law 
• Applications of Charles Law
• GayLussac’s law and its applications 
• Ideal Gas Equation
• Why Do Real Gases Deviate From Ideal Behaviour?
• Liquefaction of Gases

Index

Contents

This work is licensed under the Creative Commons Attribution-Non Commercial-No Derivatives 4.0 International License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.